Introducción
El problema de las 8 reinas es un problema matemático derivado del juego del ajedrez. Propuesto por el ajedrecista alemán Max Bezzel en 1848.
El problema
Este problema consiste en colocar, sobre un tablero de ajedrez, ocho reinas sin que ninguna de ellas pueda comerse a otra. Existen 92 maneras diferentes de colocarlas que derivan de 12 soluciones únicas. Para poder encontrarlas todas, hay que generar un árbol de soluciones mediante backtracking.
Planteamiento
Hay que tener en cuenta el movimiento de esta pieza que, como seguramente sabrás, puede moverse el número de casillas que quiera tanto en horizontal y vertical, como en diagonal. De modo que ninguna reina puede estar en la misma fila, misma columna o misma diagonal que otra.
Para su solución, es conveniente el uso de vectores. Consideraremos también la primera casilla como la superior izquierda y las filas aumentando hacia abajo, y las columnas aumentando hacia la derecha.
Se usaría un vector con 8 números enteros para indicar las posiciones de las reinas en el tablero de modo que el primer número se correspondería con la posición de la primera reina dentro de la primera fila, es decir, la columna en la que estaría la reina dentro de la primera fila. El segundo número se correspondería con la posición de la segunda reina dentro de la segunda fila y así continuaríamos hasta la octava reina en la octava fila. Es decir, teniendo el siguiente vector:
(3, 1, 6, 2, 8, 5, 4, 7)
Las reinas quedarían colocadas de la siguiente manera:
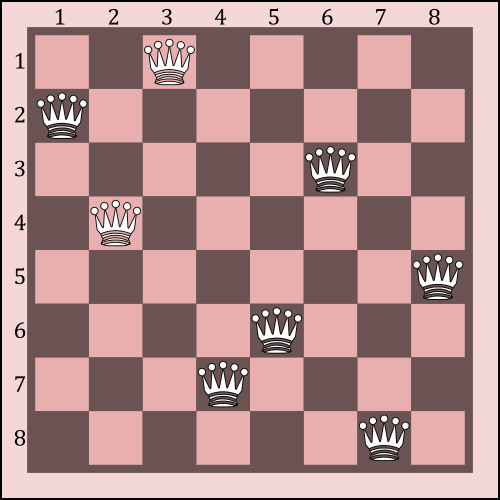
Disposición de las reinas según el vector (3, 1, 6, 2, 8, 5, 4, 7)
Es fácil ver que la solución pasará por encontrar las permutaciones sin repetición de los ocho primeros números enteros (8! = 40320 posibilidades). Ahora bien, aquí no estaríamos teniendo en cuenta las diagonales.
Para las diagonales podríamos observar el tablero y separarlas siguiendo el siguiente criterio:
- Las diagonales descendentes serían las que van de una casilla a la casilla de la siguiente columna y siguiente fila.
- Las diagonales ascendentes serían las que van de una casilla a la siguiente columna pero en una fila anterior.
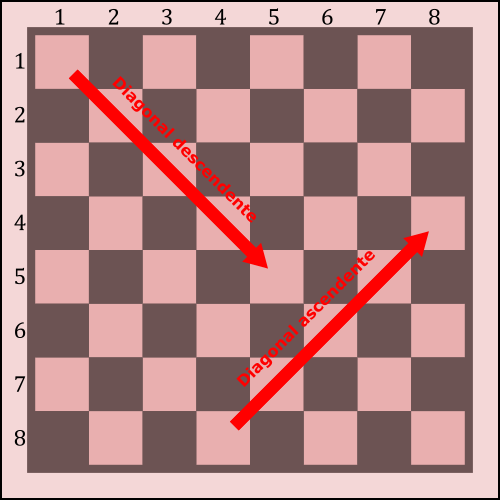
Diagonales del tablero
Con esto en mente, se puede comprobar que en una misma diagonal descendente, todas las casillas cumplen que la diferencia entre el número de fila y el número de columna es constante: i - j = k. Siendo i el número de fila y j el número de columna.
Del mismo modo, en las columnas ascendentes todas las casillas cumplen que la suma del número de fila y el número de columna es constante: i + j = k
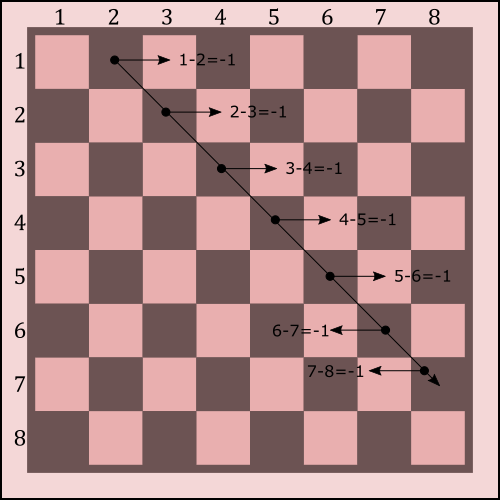
i-j=k=\text{cte.}
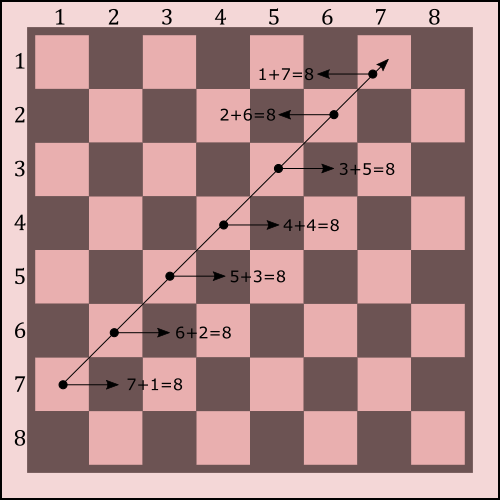
i+j=k=\text{cte.}
Ya, con esto, podemos empezar a plantear la solución al problema.
Solución
Partiendo de no tener ninguna reina colocada, que podríamos considerar la fila 0 o nodo raíz, se colocaría la primera reina generando el primer nodo del árbol. Para la siguiente fila se coloca la siguiente reina con las restricciones mencionadas anteriormente generando un nuevo nodo. Iterando de esta manera se llegaría a una solución o a un punto en el que no se podría continuar y habría que volver marcha atrás para seguir buscando posiciones.
Es decir, si colocamos la primera reina en la columna 1, el vector quedaría de la forma (1, , , , , , , ). Ahora sabemos que la siguiente reina que estaría en la fila 2 (índice 2 del vector) no podría estar en la columna 1, por ser la misma columna. Como la primera reina está en la fila 1, columna 1, la diagonal descendente es aquella en la que la resta de la fila menos la columna da 0 (1-1=0) por lo que estando en la fila 2 no podríamos colocar la reina en la casilla 2 ya que 2-2=0. La colocamos entonces en la casilla 3, quedando el vector: (1,3, , , , , , ).
Ahora, en la tercera fila, no podríamos colocar la reina en la columna 1, ni en la 3. Para ver si se puede colocar en la 2 hay que ver las diagonales ascendentes y descendentes de las dos reinas ya coloccadas.
Reina 1:
– Diagonal descendente: i-j=1-1=0
– Diagonal ascendente: no tiene
Reina 2:
– Diagonal descendente: i-j=2-3=-1
– Diagonal ascendente: i+j=2+3=5
Como estamos en la fila 3, no podríamos colocar la reina en la columna 2 ya que 3+2=5 (diagonal aescendente de la reina 2. Tampoco en la posición 4 ya que 3-4=-1 (diagonal descendente de la reina 2). Por lo que tendríamos que colocarla en la posición 5, quedando el vector solución de la siguiente forma: (1,3,5, , , , , ).
Ahora habría que sumar a las restricciones que ya teníamos, las de la reina 3.
Reina 3:
– Diagonal descendente: i-j=3-5=-2
– Diagonal ascendente: i+j=3+5=8
La reina de la fila 4 tendría restringidas las posiciones 1, 3 y 5. Veamos el resto de columnas:
Posición 2: 4-2=2; 4+2=6
Como no coincide con ninguna de las diagonales, podríamos colocarla ahí: (1,3,5,2, , , , ). El tablero quedaría así:
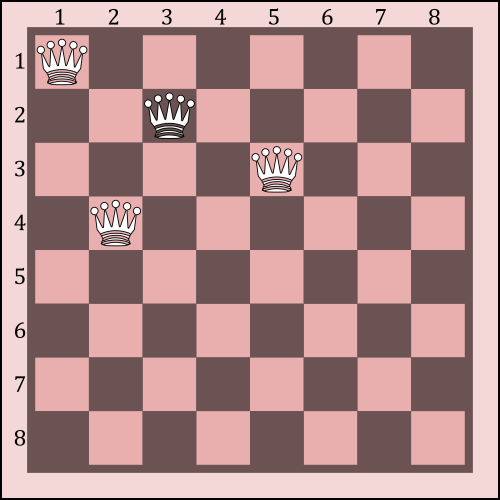
(1,3,5,2, , , , )
La siguiente reina, índice del vector 5 (fila 5) tendría bloqueadas las posiciones 1, 2, 3 y 5 por coincidir con las columnas de las otras reinas. Además, la última reina que colocamos (reina 4) añadía las siguiente restricciones en las diagonales:
Reina 4:
– Diagonal descendente: i-j=4-2=2
– Diagonal ascendente: i+j=4+2=6
Veamos en que columna podríamos colocarla:
Posición 4: 5-4=1; 5+4=9.
Como no coincide con ninguna diagonal, podríamos colocarla ahí, quedando el vector: (1,3,5,2,4, , , )
Y las nuevas restricciones:
Reina 5:
– Diagonal descendente: 5-4=1
– Diagonal ascendente: 5+4=9
Vamos ahora a probar con la reina de la fila 6, reina 6:
Posiciones bloqueadas por columnas: 1, 2, 3, 4 y 5.
Esto nos deja solamente las posiciones 6, 7 y 8 para probar las diagonales:
Posición 6: i-j=6-6=0. No se puede por ser la diagonal descendente de la reina 1.
Posición 7: i-j=6-7=-1. No se puede por ser la diagonal descendente de la reina 2.
Posición 8: i-j=6-8=-2. No se puede por ser la diagonal descendente de la reina 3.
Por lo que no podríamos colocar esta reina. Se ve claramente en el tablero:
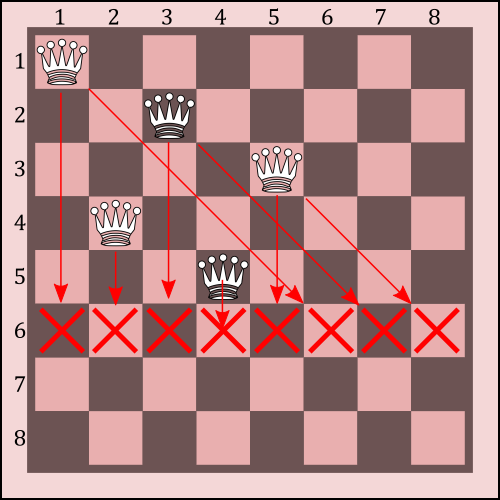
Ahora habría que dar marcha atrás a un paso anterior y probar una nueva posición. Esto haría un recorrido en profundidad del árbol de nodos buscando un vector que sea solución del problema.
Esto es un buen ejemplo del uso de algoritmos para la resolución de problemas. Este problema se puede implementar en una computadora para poder encontrar todas las soluciones posibles. En este caso, para 8 reinas, se pueden encontrar 92 soluciones. También se puede generalizar al problema de n reinas que habría que colocar en un tablero de n\times n.
Implementación
C++
#include <iostream>
#include <sstream>
#include <cstdio>
#include <vector>
#include <algorithm>
#define NREINAS 8 // dimensiones del tablero y número de reinas
using namespace std;
vector<int> sol;
int nro_sol=1;
inline bool contiene(const vector<int>& v, const int val)
{
return find(v.begin(), v.end(), val) != v.end();
}
void reinas(int k, vector<int> col, vector<int> diag45, vector<int> diag135)
{
if( k == NREINAS )
{
printf("%3d:", nro_sol++);
for(int j=0; j<NREINAS; j++) cout << " (" << j+1 << "," << sol[j] << ")";
cout << endl;
}
else
{
for(int j=1; j<=NREINAS; j++)
if( !contiene(col, j) && !contiene(diag45, j-k) && !contiene(diag135, j+k) )
{
sol[k] = j;
col.push_back(j);
diag45.push_back(j-k);
diag135.push_back(j+k);
reinas(k+1,col, diag45, diag135);
col.pop_back();
diag45.pop_back();
diag135.pop_back();
}
}
}
int main() {
cout << "SOLUCIONES AL PROBLEMA DE LAS " << NREINAS << " REINAS"<<endl;
sol.resize(NREINAS);
reinas(0, vector<int>(), vector<int>(), vector<int>());
return 0;
}
Fuente: Wikipedia (https://es.wikipedia.org/wiki/Problema_de_las_ocho_reinas)
En esta implementación, en lugar de escribir un vector, escribe pares de valores en los que el primer elemento es el número de fila y el segundo elemento es la columna (Probado con Visual Studio). Se puede jugar con el tamaño del tablero haciendo el problema ampliable a las reinas que queramos modificando el parámetro NREINAS de la línea 6. Con un valor de 9, arroja 352 soluciones. Con 10, 724 soluciones. Con 25 reinas, lo tuve que parar tras 25 minutos de ejecución y había encontrado 2605 soluciones.

Muy interesante!!